Понимание, что в большинстве систем управления не требуется строгая математическая модель объекта управления обусловило научный поиск в области нечеткого представления и оперирования информацией. Нечеткая логика как научное направление появилось в шестидесятых годах прошлого века и успела испытать времена и надежд, и забвения, и бума. Сам термин «нечеткая логика» (fuzzy logic) введен американским профессором Лотфи Заде в 1965 году в работе «Нечеткие множества» в журнале «Информатика и управление». Особый импульс направлению дали работы японских ученых, поддержанные государственной программой развития данного направления. В результате появились массовые технологические решения, базирующиеся на нечеткой логике. Не догадываясь об их присутствии в бытовых приборах, мы являемся их активными пользователями. Так они используются:
- Распознавание рукописных символов в карманных компьютерах (записных книжках) (Sony).
- Однокнопочное управление стиральными машинами (Matsushita, Hitatchi).
- Распознавание рукописных текстов, объектов, голоса (CSK, Hitachi, Hosai Univ., Ricoh).
- Управление метрополитенами для повышения удобства вождения, точности остановки и экономии энергии (Hitachi).
- Оптимизация потребления бензина в автомобилях (NOK, Nippon Denki Tools).
- Повышение чувствительности и эффективности управления лифтами (Fujitec, Hitachi, Toshiba).
- Эффективное и стабильное управление автомобильными двигателями, управление экономичной скоростью автомобилей (Nissan, Subaru).
- Оптимизированное планирование автобусных расписаний (Toshiba).
- Системы архивации документов (Mitsubishi Elec.).
- Системы прогнозирования землетрясений(Japan).
- Диагностика рака (Kawasaki Medical School) [1,2].
Несколько иной путь развития наблюдается в США, там нечеткая логика используется в системах для большого бизнеса и военных. К задачам, решаемым на базе нечеткой логики, относят анализ новых рынков, биржевой игре, оценку политических рейтингов, выборе оптимальной ценовой стратегии и т.п. Появились и коммерческие системы массового применения.
Рассмотрим суть нечеткой логики. Пусть E - универсальное множество, x - элемент E, а R - определенное свойство. Обычное (четкое) подмножество A универсального множества E, элементы которого удовлетворяют свойство R, определяется как множество упорядоченной пары A = {mA (х)/х}, где mA(х) - характеристическая функция, принимающая значение 1, когда x удовлетворяет свойство R, и 0 - в другом случае.
Нечеткое подмножество отличается от обычного тем, что для элементов x из E нет однозначного ответа "нет" относительно свойства R. В связи с этим, нечеткое подмножество A универсального множества E определяется как множество упорядоченной пари A = {mA(х)/х}, где mA(х) - характеристическая функция принадлежности (или просто функция принадлежности), принимающая значение в некотором упорядоченном множестве M (например, M = [0,1]) [5].
Нечеткий вывод занимает центральное место в нечеткой логике и системах нечеткого управления. Процесс нечеткого вывода представляет собой некоторую процедуру или алгоритм получения нечетких заключений на основе нечетких условий или предпосылок с использованием рассмотренных выше понятий нечеткой логики. Этот процесс соединяет в себе все основные концепции теории нечетких множеств: функции принадлежности, лингвистические переменные, нечеткие логические операции, методы нечеткой импликации и нечеткой композиции [5].
Системы нечеткого вывода предназначены для реализации процесса нечеткого вывода и служат концептуальным базисом всей современной нечеткой логики. Достигнутые успехи в применении этих систем для решения широкого класса задач управления послужили основой становления нечеткой логики как прикладной науки с богатым спектром приложений.
Системы нечеткого вывода позволяют решать задачи:
- автоматического управления;
- классификации данных,
- распознавания образов;
- принятия решений;
- машинного обучения и многие другие.
В рамках данного статьи рассмотрим реализацию принятия решения алгоритма нечеткого вывода Мамдани в отношении надежности банка на основе длительности его работы в среде Mathcad. Алгоритм разработан английским математиком Е. Мамдани в 1975 г. в рамках решения задачи повышения эффективности управления паровым двигателем (задачи совершенно из другой области, нежели поставленная нами, что демонстрирует универсальность подхода).
Общая логика нечеткого моделирования включает четыре этапа:
1. Введение нечеткости (фазификация). На данном этапе осуществляется разработка входных и выходных лингвистических переменных.
2. Нечеткий вывод. Вычисленное значение истинности для предпосылок каждого правила применяется к заключениям правил. Это дает нечеткое подмножество для переменной вывода каждого правила.
3. Композиция. Все нечеткие подмножества, определенные для каждой переменной вывода (во всех правилах), объединяются вместе и формируют одно нечеткое подмножество для каждой переменной вывода.
4. Приведение к четкости или скаляризация (дефазификация) результата композиции, т.е. переход от нечеткого подмножества к скалярным значениям. При этом скаляризация может проводится различными методами, например, расчетом «центра тяжести» или первого максимума [2-4,5].
Введем лингвистические переменные, которые в теории нечётких множеств, представляет собой переменную, значением которой являются фразы из естественного или искусственного языка. Данные фразы описываются посредством нечеткими множествами.
Итак, на первом этапе были сформулированы входная («Длительность работы банка») и выходная («Надежность банка») лингвистические переменные.
Проанализировав данные, был выведен диапазон длительности работы банков, который находится в интервале от 5 лет до 15 лет, посредством частотного анализа по результатам опроса респондентов установлены значения функции принадлежности для нечетких переменных «малая» (b_l(n)), «средняя» (b_m(n)) и «большая» (b_h(n)) длительность.
Лингвистическая переменная «Надежность банка» включает три нечеткие переменные «низкая», «средняя» и «высокая» надежность и оценена по пятибалльной шкале. Функции принадлежности были определены посредством частотного анализа соответствующего опроса, формулы описания нечетких подмножеств лингвистической переменной «надежность банка» (рис.1)
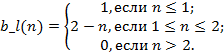
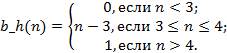
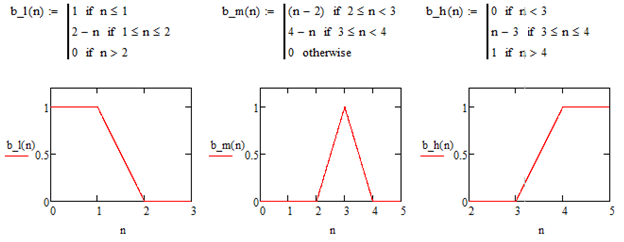
Рисунок 1 - Терм-множества лингвистической переменной "Надежность банка"
Лингвистическая переменная «Длительность работы банка» также включает три нечеткие переменные: «низкая», «средняя» и «высокая» стоимости, формулы описания нечетких подмножеств (рис.2.)
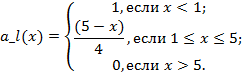
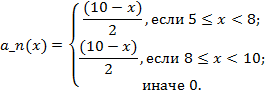
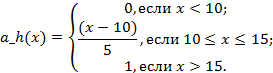
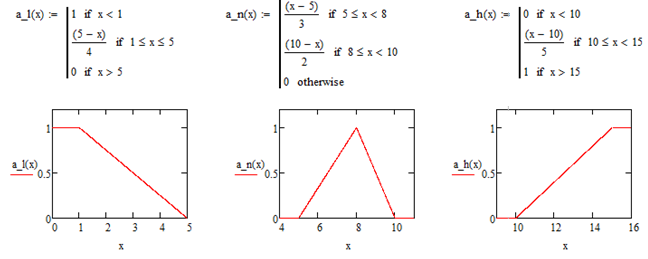
Рисунок 2 - Терм-множества лингвистической переменной "Длительность работы банка"
Далее были установлены следующие правила:
1.Если длительность работы банка маленькая, значит его надежность низкая.
2.Если длительность работы банка средняя, значит его надежность средняя.
3.Если длительность работы банка большая, значит его надежность высокая.
В качестве алгоритма вывода был выбран классический алгоритм Мамдани. Итоговое нечеткое подмножество для переменной вывода «Надежность банка» с функцией принадлежности определяется формулой:
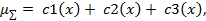
где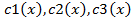
- найденные усеченные функции, полученные в соответствии с введенными правилами.
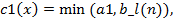
где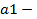 
значение функции принадлежности b_l(n), соответствующее значению входного параметра.
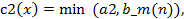
где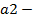 
значение функции принадлежности b_m(n), соответствующее значению входного параметра.
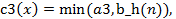
где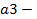 
значение функции принадлежности b_h(n), соответствующее значению входного параметра.
Дефаззификация осуществлялась на основе метода «центра тяжести».
Касаясь возможной программной реализации решения поставленной задачи, отметим следующее. В настоящее время на рынке программного обеспечения существует целый ряд специальных средств, поддерживающих аппарат нечеткой логики.
Для решения поставленной задачи был выбран универсальный математический пакет Mathcad, а точнее его свободно распространяемая версия (PTC MathcadExpress).
Ниже на рисунках представлен фрагменты листинга программы в Mathcad, демонстрирующий этап дефазификации, для оценки надежности банка с длительностью работы 8 лет (см. рис. 3).
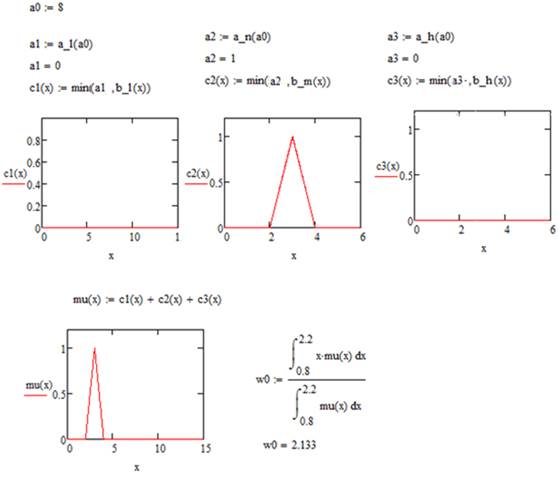
Рисунок 3 - Пример расчета надежности банка
Таким образом мы получаем, что надежность банка w0 с длительностью работы 8 лет равна 2,133.
Дефаззификация может быть выполнена:
- методом центра тяжести;
- методом центра тяжести для одноточечных множеств;
- методом центра площади;
- методом левого модального значения;
- методом правого модального значения;
- методом первого максимума;
- методом центрального максимума.
Рассмотренный алгоритм нечеткого вывода Мамдани является классикой и базой для остальных. На сегодня популярны другие системы нечеткого вывода, среди которых наиболее известны четыре:
- алгоритм Ларсена (особенность - импликация моделируется с использованием операции умножения);
- алгоритм Сугено (особенность - правые части правил вывода представлены в виде линейных функций);
- алгоритм Цукамото (особенность - функции принадлежности являются монотонными);
- так называемый упрощенный вывод (особенность – правая часть правил – четкое значение).
Выбор алгоритма зависит от характера взаимосвязей и описания нечетких переменных, а также целями моделирования (интерпретация и объяснение принятого решения или точность идентификации нелинейных зависимостей).
Рассмотренный алгоритм легко адаптировать к алгоритму Ларсена. Сам же алгоритм Мамдани прост и легок в реализации, однако добавление входных лингвистических переменных усложняет алгоритм в связи с необходимостью проработки семантики их взаимосвязей. При этом усложняется вопрос калибровки модели, что является предметом следующей работы.
Рассмотренный алгоритм Мамдани, а также упомянутые в данной статье другие алгоритмы, реализованы в надстройках математических пакетов и специализированном программном обеспечении, что скрывает от пользователей содержание этапов решения, но при этом обеспечивая простоту их использования. Рассмотренный же в настоящей статье способ реализации носит, прежде всего, теоретических характер, позволяющий раскрыть суть нечеткого вывода.
Библиографическая ссылка
Копырина Т.О., Курзаева Л.В. К ВОПРОСУ О РЕАЛИЗАЦИИ АЛГОРИТМА МАМДАНИ В MATHCAD // Международный студенческий научный вестник. – 2017. – № 6. ;URL: https://eduherald.ru/ru/article/view?id=17924 (дата обращения: 20.04.2024).