В настоящее время в связи с решением современных задач управляемых колебательных процессов особое место занимает активно развивающаяся теория многоканальных генераторов различной природы в управляемой динамике механических систем. Важной задачей является создание систем управления, обеспечивающих устойчивое движение объекта по траекториям различного вида. Построенная в работе система имеет инвариантное асимптотически устойчивое многообразие, являющееся поверхностью уровня некоторой функции [1]. Траектории системы не могут пересечь многообразие, что приводит к стабилизации движений системы в его окрестности. В таких системах возникают автоколебания. Работа представляет интерес для траекторных задач в робототехнике [4], при управлении автоколебательными мультивибраторами. В фазовом пространстве системы наблюдается образование устойчивых предельных циклов – траекторий движения точек стопы шагающего движителя [5]. Автоколебательные мультивибраторы относятся к генераторам релаксационного типа, у которых форма генерируемых колебаний резко отличается от синусоидальной.
Постановка задачи. Рассмотрим систему автоколебаний. Модель такого типа можно представить в следующем виде
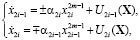(1)
где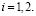 
Построенная вектор-функция управления
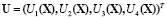
должна обеспечить стабилизацию системы по четырем каналам в окрестности многообразия W, определяемого уравнением
.
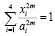Требуемые управления с обратной связью ищутся в виде:
для каналов первой подсистемы
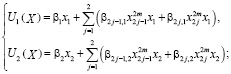
для каналов второй подсистемы
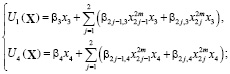
Далее задача сводится к нахождению управляющих параметров.
Метод решения. Применяя схему вывода [1], получим коэффициенты управления:
для первой подсистемы
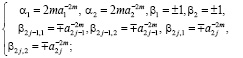(2)
для второй подсистемы
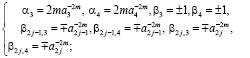(3)
где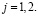 
Для этого использовалось следующее условие инвариантности многообразия ?:
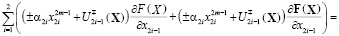
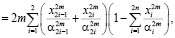
где знаки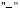 
либо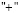 
берутся перед коэффициентами управляющих функций 
, 
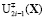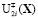, в зависимости от того 
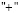либо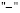 
стоят перед членами первой степени 
, 
, 
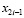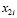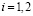, управления.
Таким образом, при выполнении соотношений (2), (3) на управляемые параметры, поверхность W будет являться инвариантным многообразием системы (1).
В частности, управления
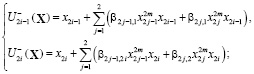
при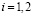 
, будут стабилизировать траектории движения в окрестности многообразия W.
Следовательно, поверхность ? является инвариантным асимптотически устойчивым многообразием [3] системы управления (1).
Численное моделирование. В работе рассмотрен ряд таких моделей автоколебательного типа посредствам изменения значений коэффициентов функций управления. Каждый из случаев был проиллюстрирован при различных начальных условиях:
Например, при начальных условиях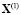 
, 
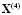, интегральные трубки в подпространстве первой подсистемы приведены на рис. 1, второй подсистемы – на рис. 2.
По фрагментам численного моделирования, отвечающим различным начальным условиям, в каждой из рассмотренных задач можно оценить время стабилизации траекторий движения. Устойчивые предельные циклы, принадлежащие этим поверхностям, представляют собой замкнутые гладкие кривые по форме, близкой к прямоугольной.
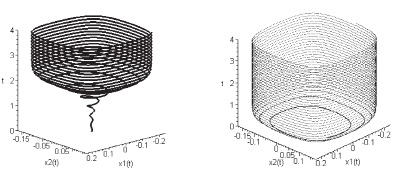
Рис. 1. Интегральные трубки в подпространстве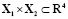 
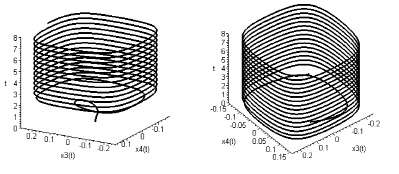
Рис. 2. Интегральные трубки в подпространстве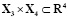 
Заключение. Получены стабилизирующие управления для решения задач управления нелинейными системами. Результаты проведенных исследований могут быть использованы при проектировании систем управления робототехническими комплексами, при проектировании детектирующих устройств переходных процессов движения по траекториям с участками близкими к прямолинейным [3, 4].