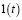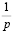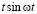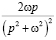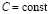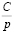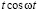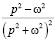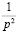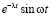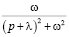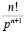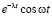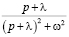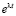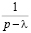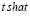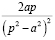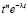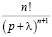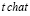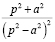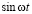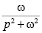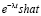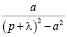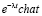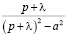Основной смысл использования метода, основанного на использовании таблицы преобразований Лапласа для расчета переходных процессов заключается в том, что f(t) некоторой вещественной переменной t ставится в соответствие функция F(p) комплексной переменной. В итоге имеем, что производные и интегралы от вещественной функции заменяют математическими функциями. В ходе расчета данных уравнений мы находим изображения, а затем, путем обратного преобразования, – оригиналы. Главным этапом практического применения является необходимость определения только независимых начальных условий, что заметно упрощает расчет переходных процессов в электрических цепях высокого порядка по сравнению с классическим методом [2, 3].
В данной статье мы рассмотрим способ применения преобразований Лапласа для расчета переходных процессов в RC-цепочке.
Для расчетов используется схема (рисунок), имеющая источник ЭДС ε, ключ K, резистор R и последовательно включенный конденсатор C. В исходном состоянии цепь разомкнута, ток отсутствует [4, 6].
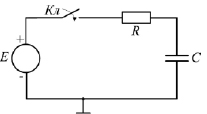
RC-цепь для расчета переходных процессов
Рассмотрим переходный процесс, который возникает, когда ключ K замыкается.
Предположим, что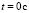 
. Появляется ток, конденсатор начинает заряжаться. В любой производный момент времени мы можем записать уравнение по правилу Кирхгофа [5, 6].
Получаем:
.
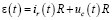Для расчета воспользуемся таблицей преобразования Лапласа.
Таблица преобразований Лапласа
|
№ |
f(t) |
F(p) |
№ |
f(t) |
F(p) |
|
1 |
|
|
11 |
|
|
|
2 |
|
|
12 |
|
|
|
3 |
t |
|
13 |
|
|
|
4 |
tn |
|
14 |
|
|
|
5 |
|
|
15 |
|
|
|
6 |
|
|
16 |
|
|
|
7 |
|
|
17 |
|
|
|
8 |
|
|
18 |
|
|
Вспомним основное уравнение для конденсатора:
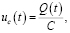
где C – емкость конденсатора, Q – заряд, который образуется в следствии протекания тока через конденсатор.
После преобразования (таблица) уравнение можно записать в следующем виде:
.
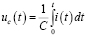Таким образом, мы приводим уравнение к дифференциальному виду. Окончательно получаем:
.
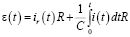Данное уравнение необходимо решить. Для этого мы вновь воспользуемся таблицей преобразований (таблица) к обоим частям уравнения.
.
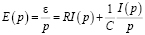Таким образом, преобразование Лапласа позволяет нам исключить время и найти образ I(p) , после чего, используя таблицу, привести уравнение к явному виду [1].
Упростим выражение, разделив обе части уравнения на общий знаменатель. Получим:
.
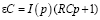Отсюда находим образ тока:
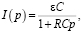
где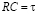 
– постоянная времени
Чтобы прийти к каноническому виду разделим и умножим знаменатель на τ. Получим:
.
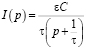В итоге получаем:
.
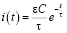Осталось найти напряжение на емкости, которое всегда равно:
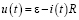
или
.
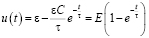Для решения данного уравнения мы не использовали ничего, кроме таблицы преобразований Лапласа.
Рассмотрим еще одну показательную задачу электротехники, решаемую с помощью операционного исчисления.
Найти закон изменения тока i(t) при включении постоянной э.д.с. E0 в последовательный колебательный контур с параметрами R, L и С при условии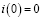 
.
По закону Кирхгофа для мгновенных значений запишем
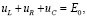
где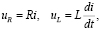 
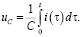
После подстановки получим дифференциально-интегральное уравнение
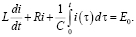
Обозначим изображение функции-оригинала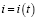 
через I(p), то есть
.
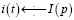Тогда по правилу дифференцирования оригинала и правилу нахождения изображения интеграла от данной функции-оригинала находим
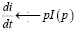
и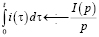 
,
а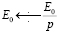 
.
Подставив найденные изображения, получим операторное уравнение
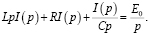
Решая это алгебраическое уравнение относительно изображения I(p), имеем
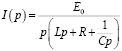
или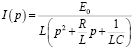 
.
Обозначим
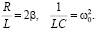
Тогда, выделяя полный квадрат в знаменателе, получим
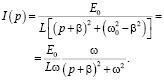
По таблице с учетом свойства линейности восстановим оригинал
.
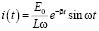Вывод. В реальном колебательном контуре существуют свободные колебания тока, которые носят затухающий характер (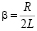
– коэффициент затухания).